排序算法

[TOC]

各种算法的比较

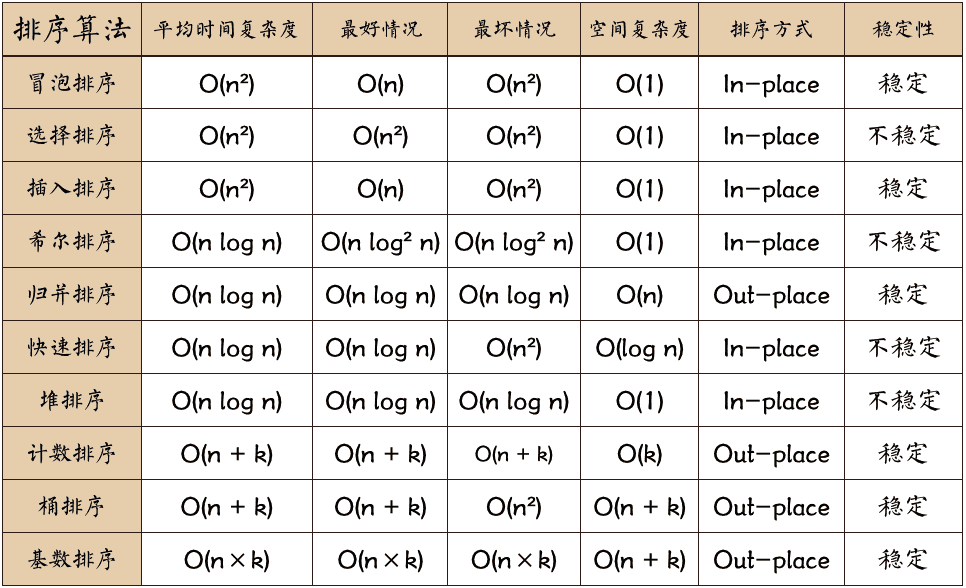
常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。用一张图概括：¹

快速排序

快速排序由东尼·霍尔在1960年提出。它的基本思想是“分治法”（Divide and Conquer）。

快速排序的平均时间复杂度为 $O(n \log_2 n)$，在最坏的情况下（例如，当输入数组已经是正序或逆序时）时间复杂度为 $O(n^2)$。但是通过随机选择枢轴或使用其他策略选择枢轴，可以最大限度地减少最坏情况发生的概率。

该排序方法被认为是目前最好的一种内部排序方法。

（1）基本思路

1. 选择枢轴：从数组中选择一个元素作为枢轴，快速排序的效率部分依赖于枢轴的选择。枢轴可以是数组中的第一个元素、最后一个元素、中间元素，或者通过某些策略（如“三数取中”）来选择。

2. 分区：重新排列数组，使得所有小于枢轴的元素都移动到枢轴的左边，所有大于枢轴的元素都移动到枢轴的右边。在这个过程结束后，枢轴会位于其最终排序完成后的位置。

   分区操作的一种常见思路如下：²（下一节中的代码也有另一种思路的实现，Drawing中的快排代码又是用的第三种思路，所以分区的方法很多）

   • 从数组两端开始，左指针往右移动，直到找到一个大于或等于枢轴的元素。
   • 右指针往左移动，直到找到一个小于或等于枢轴的元素。
   • 如果左指针仍在右指针的左边，交换这两个元素的位置。
   • 重复此过程，直到左指针和右指针相遇，这时所有小于枢轴的元素都在左边，所有大于枢轴的元素都在右边。

3. 递归排序：将枢轴左边和右边的子数组递归地进行快速排序。因为枢轴已经处于其最终位置，所以不包括枢轴的元素。

4. 终止条件：当子数组只包含零个或一个元素时，不需要进一步的操作，因为它已经排好序了。

（2）代码实现

以下代码来自参考²：

void quick_sort(int s[], int l, int r)
{
    if (l < r)
    {
        //Swap(s[l], s[(l + r) / 2]); //将中间的这个数和第一个数交换 参见注1
        // 挖坑填数：
        int i = l, j = r, x = s[l];
        while (i < j)
        {
            while(i < j && s[j] >= x) // 从右向左找第一个小于x的数
                j--;  
            if(i < j) 
                s[i++] = s[j];
            
            while(i < j && s[i] < x) // 从左向右找第一个大于等于x的数
                i++;  
            if(i < j) 
                s[j--] = s[i];
        }
        s[i] = x;
        // 分治法：
        quick_sort(s, l, i - 1); // 递归调用 
        quick_sort(s, i + 1, r);
    }
}

注1：有的书上是以中间的数作为基准数的，要实现这个方便非常方便，直接将中间的数和第一个数进行交换就可以了。

以下代码参考《数据结构》 p274（清华大学出版社，严蔚敏）。

#include <iostream>

using namespace std;

void Qsort(int arr[], int low, int high){
    if (high <= low) return;
    int i = low;
    int j = high;
    int key = arr[low];
    while (true)
    {
        /*从左向右找比key大的值*/
        while (arr[i] <= key)
        {
        	i++;
            if (i == high){
                break;
            }
        }
        /*从右向左找比key小的值*/
        while (arr[j] >= key)
        {
        	j--;
            if (j == low){
                break;
            }
        }
        if (i >= j) break;
        /*交换i,j对应的值*/
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }
    /*中枢值与j对应值交换*/
    arr[low] = arr[j];
    arr[j] = key;
    Qsort(arr, low, j - 1);
    Qsort(arr, j + 1, high);
}

int main()
{
    int a[] = {57, 68, 59, 52, 72, 28, 96, 33, 24};

    Qsort(a, 0, sizeof(a) / sizeof(a[0]) - 1);/*这里原文第三个参数要减1否则内存越界*/

    for(int i = 0; i < sizeof(a) / sizeof(a[0]); i++)
    	{
        cout << a[i] << " ";
    }
    
    return 0;
}

参考³⁴

1. 1.0 十大经典排序算法 ↩︎

2. 快速排序 ↩︎ ↩︎²

3. 来源：Chatgpt ↩︎

4. 快速排序（Quick sort） ↩︎